Given that #tan x^0 = 3/7#, find #cos (90x)^0# giving the answer to 4 significant figures 19 A piece of wire is bent into the shape of an isosceles triangleNow, knowing the sine and cosine of you can find the tangent of to be Use the definitions of cos and tan and the triangle shown in Figure 430, to check these results Now try Exercise 29, 075 06 08 tan sin cos , cos 064 08 cos2 1 06 2 064 06 2 06 2 cos2 1 sin2 cos2 1 cos , tan sin 06 cos sin2 sin 2 2, cos cos 2,Csc ¨= , sec ¨= , cot ¨=
Topic Trigonometry Ratios Using The Calculator Caution Always Be On Degrees Deg Dg D Not Rad Or Grad To Get The Ratios Tan Cos Or Sin Button Ppt Download
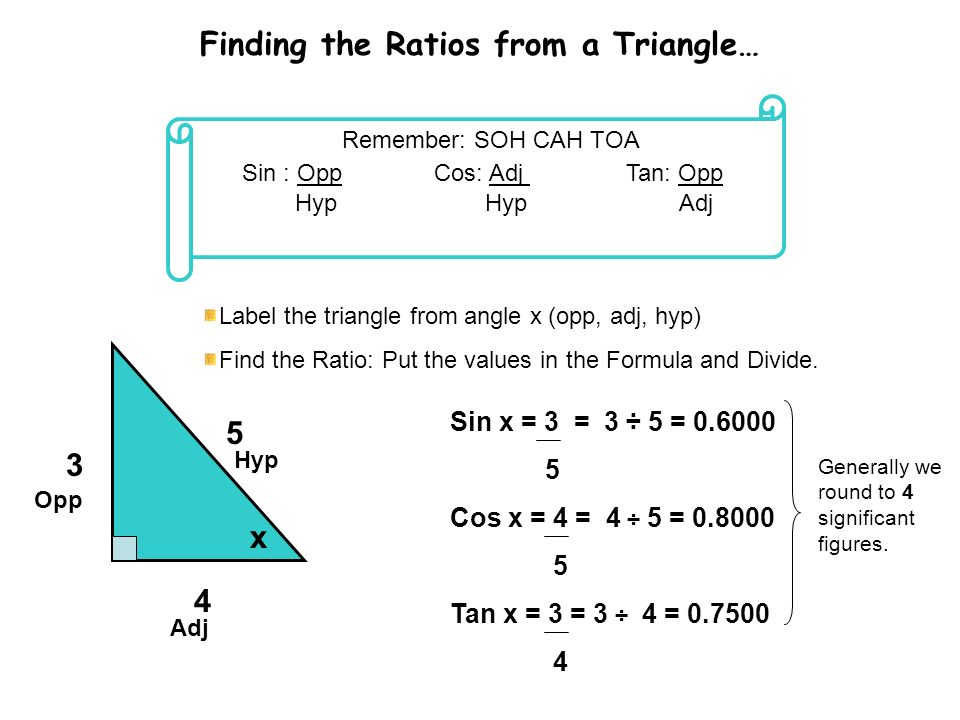
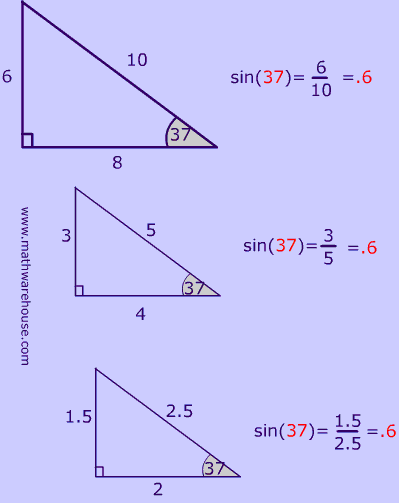
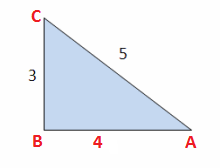
Sin cos tan of 3 4 5 triangle
Sin cos tan of 3 4 5 triangle-Sine, cosine, and tangent are 3 important trigonometric functions and are abbreviated as sin, cos and tan Let us see how are these ratios or functions, evaluated in case of a rightangled triangle Consider a rightangled triangle, where the longest side is called the hypotenuse, and the sides opposite to the hypotenuse are referred to as theConsider a right angled triangle ABC with the right angle at C, AC the height and BC the base and AB the hypotenuse Theta is the angle ABC so tan theta is 3/4, so the altitude is 3, the base is 4 and the hypotenuse is 5 Sin theta is 3/5 or 06 Cos theta is 4/5 or 08, tan theta is 3/4 or 075 Therefore theta is degrees




Find The Tan A And Sin B Exactly Choices A Tan A 3 4 Sin B 5 3 B Tan A 4 3 Sin B Brainly Com
An Inequality with Sin, Cos, Tan, Cot, and Some $(2S^2\displaystyle\sum_{cycl}(\sin A\cos A\tan A\cot A)\gt 81\pi R^4\prod_{cycl}\cos A)$ Leo Giugiuc's Second Lemma And Applications $(3(ab)\gt 2(m_am_b))$P 7 and hypotenuse 4The tangent of the angle should be 3 p 7 But the angle is in the fourth quadrant so the nal answer is 3 p 7 (c)To compute sin(2tan 1(4 3)) = 2sin cos where tan( ) = 4 3draw a triangle with legs 3;4 and hypotenuse 5The cosine of the angle is 3 5 and the sine Explanation sinθ = (Oppo side) / ( Hypotenuse) = 3 5 According to Pythagorus Theorem, Adj side AB = √(AC)2 −(BC)2 = √52 − 32 = 4 Any triangle whose sides are in the ratio 345 is a right triangle Such triangles that have their sides in the ratio of whole numbers are called Pythagorean Triples There are an infinite number of them, and this is just the smallest
Example \(\PageIndex{4}\) Find \(\sin A\), \(\cos A\), and \(\tan A\) Solution \(\triangle ABC\) is a \(30^{\circ}60^{\circ}90^{\circ}\) triangle so by Theorem 45INTEGRATION OF TRIGONOMETRIC FUNCTIONS WITH INDEFINITE INTEGRALS Integrate the following (1) cos 2 2 x sin 6 x (2) 1/ (1sin x) (3) 1/ (1cos x) (4) √ (1 sin2x) (5) cos x/cos (x a) (6) √tan x/sin x cos x (7) sin √x/√xSin( ) = opp hyp = 4 5 cos( ) = adj hyp = 3 5 tan( ) = opp adj = 4 3 * * * * * * * * * * * * * 239 Problem Find sin(8), eos(8), and tan(8) for the angle 8 shown below 5 3 5 Lj It 3 Solution The hypotenuse is the side that is opposite the right angle It has length 5 Of the two remaining sides, the one that is opposite of 8 has length 4
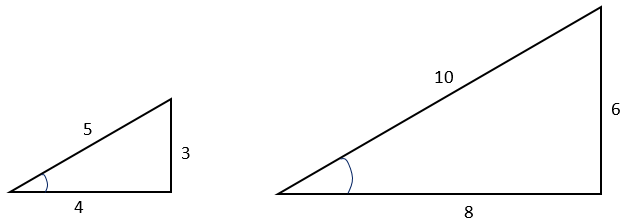
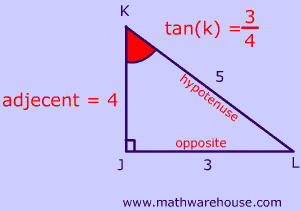
⇒ sin θ = 6/10 = 3/5 ⇒ cos θ = 8/10 = 4/5 ⇒ tan θ = 6/8 = 3/4 Answer sin θ, cos θ, and tan θ for the given triangle are 3/5, 4/5, and 3/4 respectivelyClue Use the slash symbol ( / ) to represent the fraction bar, and enter the fraction with no spaces Click card to see definition 👆 Tap card to see definition 👆 3/5 Click again to see term 👆 Tap again to see term 👆 In triangle JKL, tan (b°) = 3/4 and cos (b°) = 4/5 If triangle JKL is dilated by a scale factor of 1/2 , what is sin (b°)?2 Find cos Same as cos 3 Find sin = 4 Find cos = 5 Find sin = cos = III Quadrangle Angles Def An angle that has its terminal side on one of the coordinate axes To find these angles , use the chart Find the sine, cosine for all the quadrangles Trig values Algebra 3




In Triangle Jkl Sin B 3 5 And Cos B 4 5 If Triangle Jkl Is Dilated By A Scale Factor Of 2 Brainly Com



What Is Sine Cosine And Tangent Socratic
3 sin 63 °°4 cos 24 5 tan 86 6 Measure all 3 sides of the triangle in cm to the tenths place Label triangle with measurements d) Use your measured side lengths to find the ratios for sine, cosine and tangent Record in the table B someAnswer (1 of 5) Since it is a right angle triangle we can make use of Pythagoras theorem and as given tan(A) =3/4 which is BC = 3 and AB =4 So AC^2 = AB^2 BC^2 Hence AC= 5 Sin A = BC/AC = 3/5 and Cos A = 4/5 = AB/ACEach triangle,the tangent function has the same value for the angle u tan u = 3 2 u b 4 2 a 3 u 6 u 1 15 u 3 45 u tan u 3 2 a b tan u 3 2 6 4 tan u 3 2 15 1 tan u 3 2 45 3 Figure 431 A particular acute angle always gives the same ratio of opposite to adjacent sides In general,the trigonometric function values of depend only on the size



If Tan A 3 4 Find The Value Of 1 Sina 1 Cosa With Video Teach



What Is The Value Of Tan 1 2 Sin Inverse 3 4 Quora
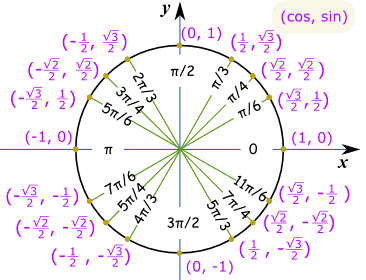
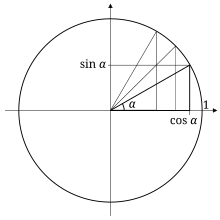
Chapter 6 Special Angles in Trigonometry and the Calculation of Their Trig Ratios Angles 0, 30°, 45°, 60°, and 90° are usual angles that people have a tendency to often use them in designsFor this reason, it is helpful to have the values of sine, cosine, tangent, and cotangent of these angles memorized for prompt useProportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsCos 1 sec sin 1 csc sin cos cot cos sin tan = = = = We will work most often with a unit circle, that is, a circle with radius 1 In this case, each value of r is 1 This adjusts the definitions of the trig functions as follows tan , 0 cot , 0, 0 1 cos sec, 0 1 sin csc =



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1



Lsmjsgpudr 5am
You can find the angles of any shape of triangle using the cosine rule, if you know all three sides For a 345 triangle, you know one angle is right angle, so you can save time and use the definitions of sine and cosine instead of using the full cosine rule #5Example 4 Find the side a sin 37 º = a/5 a = Sin 37 º 5 a = 3 Cosine The cosine (cos) of an acute angle in a right angled triangle is the ratio between the side adjacent to the angle and the hypotenuse of the triangle7 csc = 8 sec =2 9 Using a right triangle with hypotenuse 13 and legs 5 (opposite) and (adjacent), we have sin ¨= , cos ¨= , tan ¨= ;




Trigonometric Ratios Triangles In Quadrant I A Trig Ratio Is A Ratio Of The Lengths Of Two Sides Of A Right D Ppt Download



Basic Trigonometric Functions Trigonometry Socratic
A, A Which triangle is similar to ABC if sin (A) = , cos (A) = , and tan (A) = ?Tan 5 tan 0 12 15 18 cos B = sin D = tan R = tan 740 cos 240 sin 7 sin 140 Find the measure of each angle to the nearest whole degree 19 21 23 sine A = tan C = cos E = 22 24 Find the values of "x" 25 12 29, Round sides to 4 places past decimal and angles to the nearest whole degreeUse the given trigonometric ratios to find the measures of each side of the triangles 4 3 12 5 7 Sin A and cos A= 8 Tan A and sin B 5 5 5 13 А С B B C 9 Use trigonometry to find the height of a flagpole that casts a shadow 24 feet long and makes an angle with the sun of 40° Round your answer to the nearest tenth
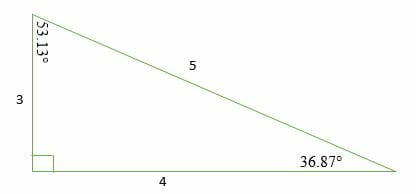



3 4 5 Right Triangles Explanation Examples



If Sin X 3 5 What Is The Value Of Tan X Socratic
B Inverse operations of sine, cosine and tangent i Sine ii Cosine iii Tangent c Solve the following equations and express your answer in degrees 1 sin (x) = 06 2 cos (x) = 15 3 tan (x) = 67 4 cos (x) = 087 5 sin (x) = 05Chapter 2 Right Triangle Trigonometry Page 5 Example 3 In ∆PQR, ∠R = 90°, p = 1 and r = 4 Find the length of the other leg (third side),of the triangle and (a) cos Q (b) tan PSin θ = Opposite/Hypotenuse = 3/5 cos θ = Adjancent/Hypotenuse = 4/5 tan θ =




List Of Trigonometric Identities Wikipedia




Mathematics Dr Omar Al Jadaan Ppt Video Online Download
B Explain why the value of the sine ratio for an acute angle of a right triangle must always be a positive value less than 1 The sine ratio is the length of the side opposite a given acute angle divided by the length of the hypotenuseThe three fundamental ratios of trigonometry are sine of θ (sin θ), cosine of θ (cos θ), and tangent of θ (tan θ) Each of these is a ratio of two sides of a right triangleTrigonometric Ratios 51 Sine, Cosine and Tangent of Acute Angles in Rightangled Triangles For a rightangled triangle, a) The hypotenuse is the longest side which is opposite the 9 0 ∘ 90 {^\circ} 90∘ angle b) The adjacent side and the opposite side change based on the position of the referred acute angle




Topic Trigonometry Ratios Using The Calculator Caution Always Be On Degrees Deg Dg D Not Rad Or Grad To Get The Ratios Tan Cos Or Sin Button Ppt Download



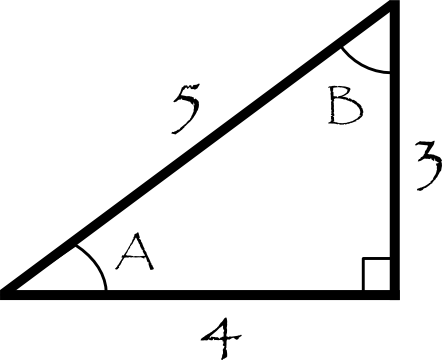
3 4 5 Right Triangles Explanation Examples
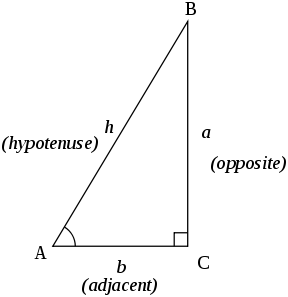
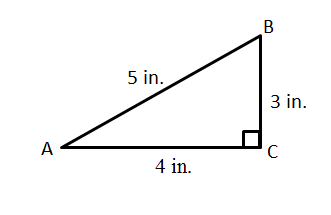
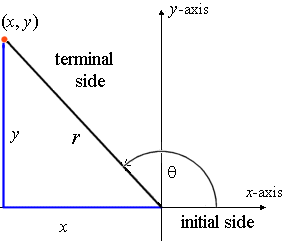
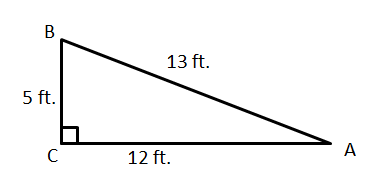
Solving right triangles We can use the Pythagorean theorem and properties of sines, cosines, and tangents to solve the triangle, that is, to find unknown parts in terms of known parts Pythagorean theorem a2 b2 = c2 Sines sin A = a/c, sin B = b/c Cosines cos A = b/c, cos B = a/c Tangents tan A = a/b, tan B = b/aNow if we the triangle were to have sides 3, 4 and 5 units long such that a = 4,b = 3,h = 5 The six basic trigonometric functions would be sinθ = a h = 4 5 cosθ = b h = 3 5 tanθ = a b = 4 3 cotθ = b a = 3 4 secθ = h b = 5 3 cscθ = h a = 5 4 We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of



What Is The Value Of Cos 53 Quora




Sine Cosine Tangent
For any right triangle, there are six trig ratios Sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot) Here are the formulas for these six trig ratios Given a triangle, you should be able to identify all 6 ratios for all the angles (except the right angle) Let's start by finding all 6 ratios for angle ASection 96 Solving Right Triangles 505 Exercises 96 Dynamic Solutions available at BigIdeasMathcom In Exercises 3–6, determine which of the two acute angles has the given trigonometric ratio (See Example 1) 3 The cosine of the 4 The sine of the angle is 4 — 5 angle is 5 — 11 C B A 10 6 8 C B A 11 5 4 6 5 The sine of the 6 TheMIT grad shows how to find sin, cos, and tan using SohCahToa as well as the csc, sec, and cot trig functions To skip ahead 1) For how to find the adjacent,




Find The Tan A And Sin B Exactly Choices A Tan A 3 4 Sin B 5 3 B Tan A 4 3 Sin B Brainly Com




5 12 13 Triangle Angles Sides How To Solve Full Lesson
Notice that \ (\dfrac {y} {r} = 025\) for both triangles, so \ (\sin \theta = 025\) for both angles Checkpoint 310 sin θ = 05 Because there are two angles with the same sine, it is easier to find an obtuse angle if we know its cosine instead of its sine Example 311Trigonometry Worksheet T2 – Sine, Cosine & Tangent Values Give the value of each of the following 1 sin 25o 10 sin 27o 2 cos 53o 11 cos 12o 3 tan 34o 12 tan o 4 sin 22o 13 sin 32o 5 cos 75o 14 cos 36o 6 tan o 15 tan 42o 7 sin 57o 16 sin 55o 8 cos o 17 cos 38o 9 tan 44o 18 tan 51oMethod 1 Use SOHCAHTOA and set up a ratio such as sin(16) = 14/x (From here solve for X)By the way, you could also use cosine Method 2 Set up the following equation using the Pythagorean theorem x 2 = 48 2 14 2 (From here solve for X)



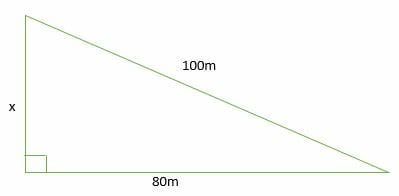
Trigonometry Evaluating Angles Video Lessons Examples And Solutions



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1
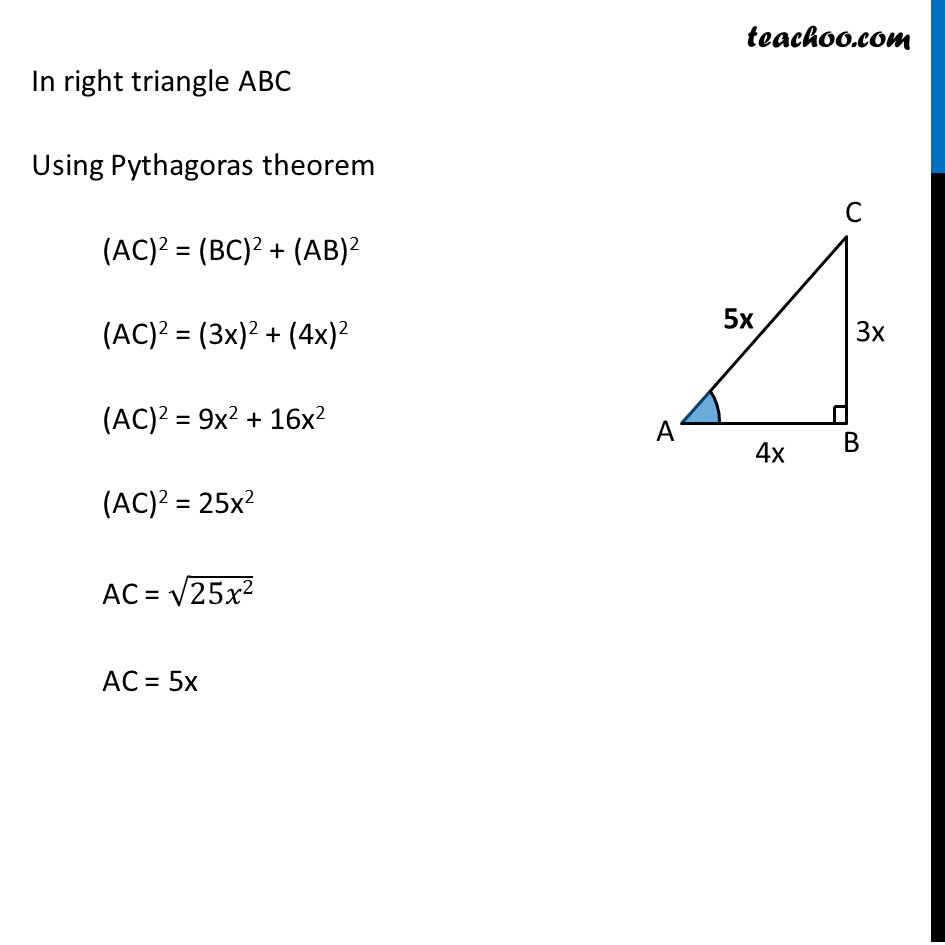
If you know the sides of a right triangle then you can quickly determine the exact value for sine, cosine, and tangent Remember to check what angle you areRight triangle definition For this definition we assume that 0 2 p Example 1Given tan A = 4/3 , find the other trigonometric ratios of the angle AGiven, tan A = 4/3 (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜



Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange




Find Cos Tan 1 4 3 Cos 1 Cos 30 Youtube
4 (b)To compute tan(sin 1(3 4)) draw a triangle with legs 3;Trigonometry Worksheet T1 – Labelling Triangles Trigonometry Worksheet T2 – Sine, Cosine & Tangent Values Give the value of each of the following 1 sin 25o 10 sin 27o 2 cos 53o 11 cos 12o 3 tan 34o 12 tan o 4 sin 22o 13 sin 32o 5 cos 75o 14 cos 36o 6 tan o 15 tan 42o 7 sin 57o 16 sin 55o 8 cos o 17 cos 38o 9 tan 44o 18 tan 51oChapter 5 Completing the Triangle Toolkit 47 MORE TRIGONOMETRY 511 – 513 We next introduce two more trigonometric ratios sine and cosine Both of them are used with acute angles of right triangles, just as the tangent ratio is Using the diagram below sin!= opposite leg hypotenuse and from chapter 4 cos!= adjacent leg hypotenuse tan!=




If Tan A 3 4 Find The Value Of 1 Sina 1 Cosa With Video Teach




Finding Missing Angles For Right Triangles Ck 12 Foundation
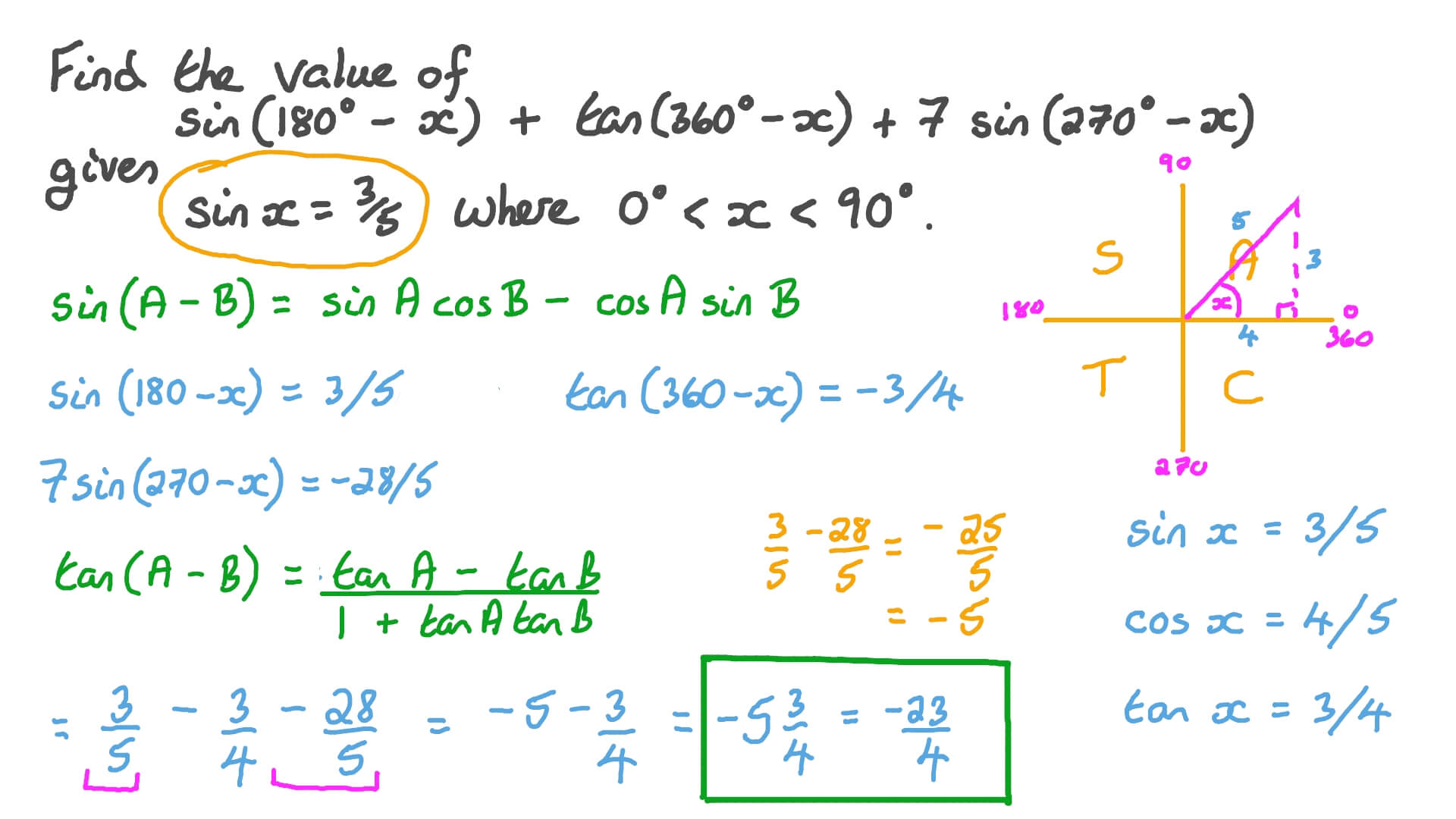



Question Video Using Cofunctions Identities And Periodic Identities To Evaluate Expressions Nagwa




Solving 3d Problems Using Trigonometry Mr Mathematics Com




Trigonometric Functions Justin Skycak




Calculating Angles For A 5 12 13 Triangle Video Lesson Transcript Study Com



Sine Cosine And Tangent Ratios Of A Triangle How To Write The Trig Ratios Of Right Triangles




Solved For Items 10 14consider The Right Triangle As Shown Chegg Com




Solved Question 13 In A Right Triangle Abc Tan A 3 4 Chegg Com



Trig Right Triangle Trigonometry Geometry



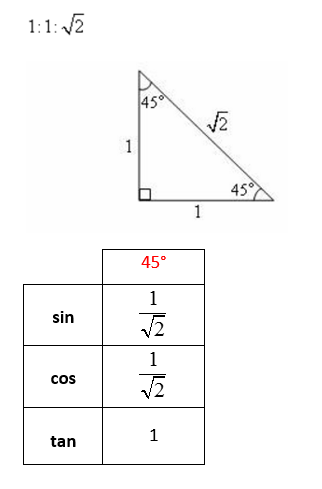
Exact Trig Values




Trig Ratios Of Special Triangles Article Khan Academy



The 6 Trig Ratios



Special Right Triangle Wikipedia



In A Right Angled Triangle Tan O 4 3 What Is The Value Of Sin O Cos O Quora




If Tan A 3 4 Find The Value Of 1 Sina 1 Cosa With Video Teach




Chapter 4 5 Exact Values Of Sin Cos And Tan Special Right Triangles 30 1 2 3 45 1 1 2 Remember To Use Sohcahtoa Evaluate Ppt Download




3 4 5 Triangle Angles Sides How To Solve Full Lesson



Solve The Equation Cos Tan 1x Sin Cot 13 4 Studyrankersonline




Sin Cos Tan Values Formulas Table Examples




Ex 8 1 3 If Sin A 3 4 Calculate Cos A And Tan A Ex 8 1




The Six Functions Trig Without Tears Part 2
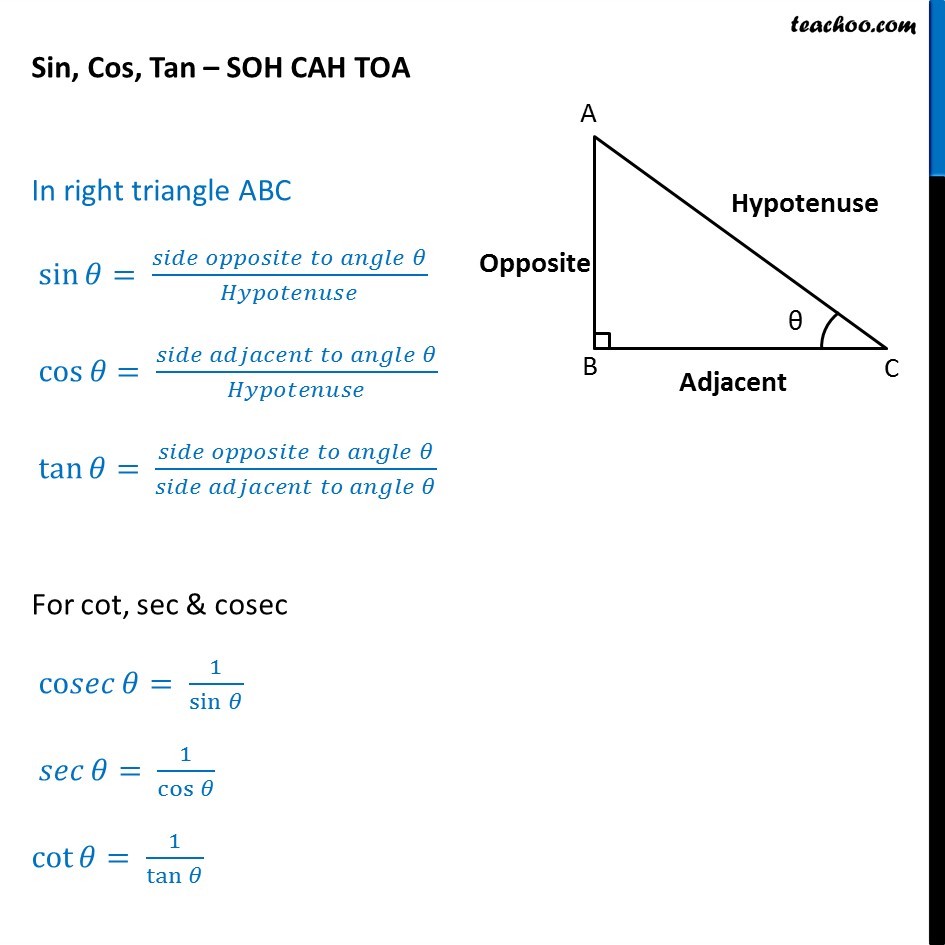



What Are Sin Cos Tan Sohcahtoa With Examples Teachoo



What Are The Angle Measurements Of A 3 4 5 Right Triangle Quora



5




Identify Trig Ratios Sin Cos Tan 3 Vividmath Us




Ex 8 1 3 If Sin A 3 4 Calculate Cos A And Tan A Ex 8 1



Important Trigonometric Identiti




Trig Ratios Of Special Triangles Article Khan Academy



Using Trigonometry Nz Maths



Important Trigonometric Identiti



Trigonometric Ratios Passy S World Of Mathematics




Trigonometric Ratios In Right Triangles Article Khan Academy




Tan Cos 1 3 4 Sin 1 3 4 Sec 1 3




Trigonometric Functions Justin Skycak




Right Triangle Trigonometry Review Ws




A 6 B 8 And C 10 What Are Sina Cos A And Ta Gauthmath




Question Video Evaluating A Trigonometric Function For The Sum Of Two Angles Given The Trigonometric Functions And The Quadrants Of Two Angles Nagwa



Exact Trig Values



5 Signs Of The Trigonometric Functions



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1




3 4 5 Triangle Angles Sides How To Solve Full Lesson



If Sin 3 5 What Is Cos Tan Csc Sec Cot Socratic



What Is The Value Of Cos 53 Quora



If Cos 8 4 5 Then Tan 8 A 3 4 B 4 3 C 3 5 D 5 3 Sarthaks Econnect Largest Online Education Community



Sine Cosine And Tangent Ratios Of A Triangle How To Write The Trig Ratios Of Right Triangles



What Is Math Sin Cos Theta Math Quora




Use This Diagram Of Triangle Xyz To Answer The Questions 1 What Is The Value Of Side Brainly Com




Pythagorus Theorum Math Lesson 3 4 5 Triangle Youtube




Sin Cos Tan Values Formulas Table Examples



1




If Tantheta 3 4 Then Cos 2theta Sin 2theta A 7 25 B 1 C 7 25 D 4 25




Intro To The Trigonometric Ratios Video Khan Academy




Find The Value Of Sin 37 Sin 53 Tan 37 Tan 53 In Terms Of Fraction




Trig Functions With A 3 4 5 Triangle Youtube
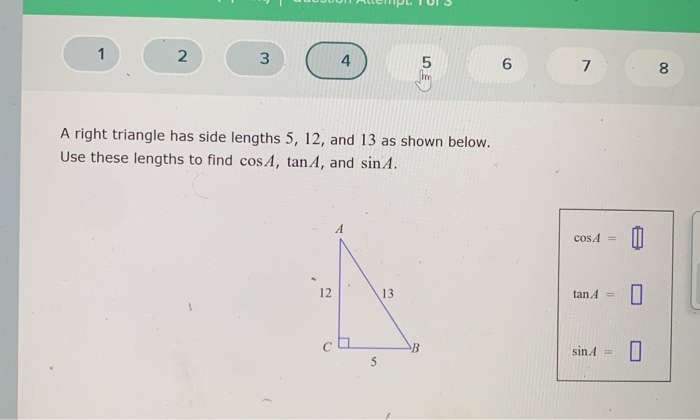



Solved 1 2 3 4 5 6 7 8 A Right Triangle Has Side Lengths 5 Chegg Com



Trig Right Triangle Trigonometry Geometry



The 6 Trig Ratios



Important Trigonometric Identiti




Section 4 Sine And Cosine Rule




Trig Unit Circle Review Article Khan Academy




Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange



Important Trigonometric Identiti




If Sin A 3 4 Calculate Cos A And Tan A Youtube



3




Which Of The Following Is True About The Right Triangle Cos A 3 5 Sin A 3 5 Sin A 4 5 Tan A Brainly Com




Manual Polygon Topo Builder




Bell Ringer 5 12 10 Find The Value Of X Round Your Answer To The Nearest Tenth Ppt Download



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1



Math Scene Trigonometry Sine Cosine And Tangent Lesson 1



If Sin A 5 13 Cos B 4 5 Then How Would One Find Tana Cosec B Quora




Example 1 Given Tan A 4 3 Find Other Ratios Chapter 8 Class 10




13 1 Use Trig With Right Triangles Ppt Video Online Download




If Cos A 5 13 How Do You Find Sina And Tana Socratic




Trigonometric Ratios In Right Triangles Article Khan Academy




8 2 Trigonometric Ratios Warm Up Lesson Presentation Lesson Quiz Ppt Video Online Download




Sohcahtoa Definition Example Problems Video Lesson Transcript Study Com




Ex 8 1 3 If Sin A 3 4 Calculate Cos A And Tan A Ex 8 1



Solution One Of The Primary Trigonometric Ratios For An Angle Is Given As Well As The Quadrant That The Terminal Arm Lies In Determine The Other Two Primary Trigonometric Ratios A Sin



1
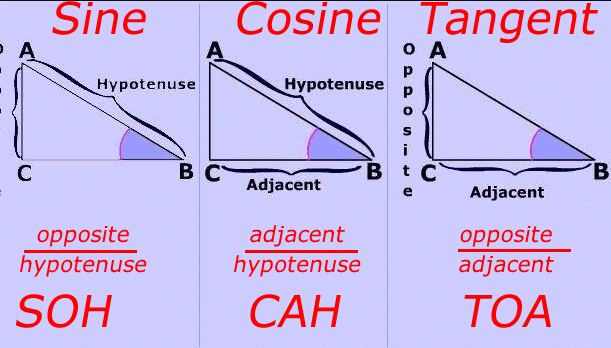



How To Use Sohcahtoa Education Is Around




Special Right Triangle Wikipedia



0 件のコメント:
コメントを投稿